Grammar Variational Autoencoder 논문 리뷰

Grammar Variational Auto-Encoder(GVAE)는 Gomez-Bomb barelli et al.(2016)¹의 VAE기반으로 생성된 신약 후보 물질들이 대부분 유효하지 않는 것에 문제를 제기하여, SMILES string 생성 문법을 직접적으로 제약 조건으로 걸어 유효한 신약 후보 물질을 생성하는 모델입니다.

Problem

신약 후보 물질의 SMILES string 생성 모델들(RNN, VAE)의 단점은 유효하지 않은 string을 생성하는 경우가 많이 발생한다는 것입니다.

• Valid String : c1ccccc1 (benzene)
• Invalid String : c1ccccc2 (??)

Gomez-Bomb barelli et al.(2016)가 제안한 VAE는 decoder를 통해 연속적인 latent space에서 discrete한 SMILES string을 생성합니다. 그러나, 유효하지 않는 string에 대한 확률이 높아지도록 학습이 된 경우, 학습이 완료가 된 후에도 계속 올바르지 않은 SMILES string이 생성되는 문제가 발생합니다.

따라서 본 논문에서는 이러한 이슈를 완화하기 위해 SMILES string을 생성하는 문법에 관한 정보를 모델에게 직접적으로 알려줌으로써 유효한 SMILES string을 생성하도록 하는 모델(Grammar VAE)을 제안하였습니다.

Context-free grammars²

SMILES string을 생성하는 문법은 문맥 자유 문법(Context-free grammar, CFG)을 따릅니다. 다른 나라 언어를 이해하거나 그 나라 언어로 대화나 글을 쓰기 위해선 문법을 이해하고 있어야 합니다. 마찬가지로 프로그래밍 언어를 이해하기 위해선 그 언어를 정의한 문법을 이해하고 있어야 합니다. 대다수 프로그래밍 언어들이 CFG기반입니다. CFG은 촘스키 위계의 type-2에 해당하는 문법입니다.

문맥 자유 문법은 $G=(V, \Sigma, R, S)$ 4개의 순서쌍으로 구성됩니다.

• V : non-terminal 심볼들의 유한집합
• $\Sigma$ : terminal 심볼들의 유한집합
• R : 생성규칙(production rules)의 유한집합
• S : 시작(start) 심볼

예를 들어, 문법 G=({A}, {a,b,c}, P, A), P : A $\rightarrow$ aA, A $\rightarrow$ abc가 있다면, 문법아래 생성될 수 있는 string은 aabc입니다. 위의 예는 단순하지만 생성 규칙에 따라 나올 수 있는 string의 경우의 수는 매우 많습니다. 이렇게 생성된 string을 tree구조로도 표현할 수 있습니다.

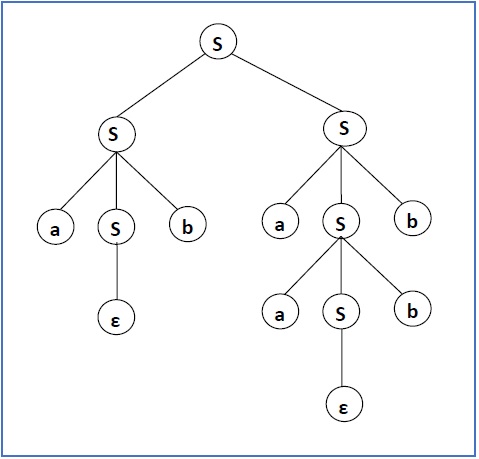
문법 G=({S}, {a,b}, P, S), P : S $\rightarrow$ SS | aSb | $\epsilon$ 이라면, 생성규칙에 따라 생성된 string중 하나는 $S \rightarrow SS \rightarrow aSbS \rightarrow abS \rightarrow abaSb \rightarrow abaaSbb \rightarrow abaabb$ 입니다. 이를 tree구조로 나타내면 아래 그림과 같습니다.

GVAE는 CFG의 아이디어를 이용한 모델입니다. CFG기반의 SMILES grammar가 있으며, encoder의 입력값은 SMILES string이 아니라 각 화합물 SMILES string을 생성하기 위해 사용된 생성규칙들입니다. 마찬가지로, decoding 결과는 SMILES string이 아니라, SMILES string에 관한 생성 규칙입니다. 시퀀스 별로 그 다음으로 나올 가능성이 높은 생성 규칙이 결과로 나옵니다. 세부적인 모델 설명은 아래와 같습니다.

Methods

본 논문에서 사용된 VAE의 encoder와 decoder는 Gomez-Bomb barelli et al.(2016)와 동일한 구조를 사용하였습니다.

encoding

위 그림은 모델의 encoder가 SMILES grammar와 함께 구현되는 과정에 관한 것입니다. 그림3의 1번은 SMILES grammar의 일부입니다. 전체 SMILES grammars는 논문 참고하시기 바랍니다. 예를 들어 벤젠 SMILES string인 c1ccccc1을 encoding 한다고 했을 때(2번), SMILES grammar에 따라 벤젠 SMILEs string의 parse tree를 구축합니다. 그런 뒤, 이 parse tree를 위에서부터 아래, 왼쪽에서 오른쪽 방향으로 생성 규칙들로 다시 분해된 후(3번), 분해된 각 규칙들은 원핫벡터로 변환됩니다(4번 그림). 이 때, 원핫벡터의 차원 $K$ 은 SMILES grammar 생성 규칙의 개수입니다. $T(X)$ 를 분해된 생성규칙들의 개수라 할 때, 벤젠의 생성규칙을 인코딩한 행렬의 차원은 $T(X)\times K$ 가 됩니다. 그 후, Deep CNN을 거쳐서, 벤젠에 대한 생성규칙을 latent space 상에 $z$ 로 맵핑합니다.

decoding

다음은 latent space상에 $z$ 로 맵핑된 벤젠 생성규칙이 어떻게 다시 discrete한 시퀀스를 가진 생성규칙들로 이뤄진 string으로 변환되는지에 관한 과정에 대한 설명입니다. GVAE에서 Decoder의 핵심은 항상 유효(valid)한 string이 나오도록 생성규칙들을 선택하는 것입니다. 먼저, 잠재 벡터 $z$ 를 RNN layer를 통과하여 시퀀스 별로 logit이 출력됩니다(그림4의 2번). logit 벡터의 각 차원은 하나의 SMILES grammar 생성규칙에 대응됩니다. 타임 시퀀스의 최대 길이는 $T_{max}$ 이며 따라서 최대로 나올 수 있는 logit 벡터의 갯수도 $T_{max}$ 입니다.

Masking Vector

decoding 결과로 출력된 일련의 생성규칙 시퀀스들이 유효하기 위해서 last-in first-out(LIFO) stack과 masking vector가 등장합니다.

그림 5.는 stack과 masking vector를 이용한 decoding과정을 나타낸 그림입니다. 제일 첫 심볼은 항상 smiles가 나와야 하므로, (1)처럼 smiles를 stack합니다. 그 다음, smiles를 뽑은 후, smiles으로 시작하는 생성규칙은 1 그 외 나머지는 0으로 구성된 masking vector를 구성한 뒤 첫번째 시퀀스 logit가 element-wise 곱을 합니다((3)). 그런 다음, 아래 mask된 분포에 따라 sampling을 하면 (4)와 같이, smiles $\rightarrow$ chain 생성규칙이 출력됩니다.

$$p(\text{x}_t = k|\alpha,\text{z}) = \frac{m_{\alpha, \,k}exp(f_{tk})}{\sum_{j=1}^Km_{\alpha, \,k}exp(f_{tj})}$$

위와 같은 방법으로 $t \rightarrow T_{max}$ 가 될 때까지, sampling을 하면 한 화합물을 구성하는 생성규칙들을 출력하였고, 결국 문법적으로 유효한 화합물을 생성한 것입니다.

Bayesian Optimization

Gomez-Bomb barelli et al.(2016)¹를 보면, 약물 특성을 포함한 latent space를 구축하기 위해, latent layer에 약물 특성을 예측하는 MLP layer를 추가하여 학습을 진행합니다. 마찬가지로, 약물 특성이 담긴 latent space를 구축하기 위해 VAE 학습 완료 후, Sparse Gaussian Process(SGP)를 이용하여 예측모델을 학습합니다. 여기서 사용된 약물 특성은 penalized logP 입니다.

Experiment Result

GVAE 모델의 성능은 Gomez-Bomb barelli et. al.(2016)¹와 유사한 VAE인 Character VAE(CVAE) 성능과 비교하였습니다. 정성적인 평가를 위해, 임의의 수학표현식을 생성하여 유효한 수학표현식을 만드는지를 확인하였습니다.

<그림 6.>의 Table 1.은두 모델의 embedding 공간의 smoothness를 보여주는 결과입니다. 각각 두 개의 식(볼드체)을 encoding 한 뒤, latent space 상의 두 점을 선형보간법(linear interpolation)을 한 것입니다. 보시면, GVAE는 100% 유효한 수학식이 공간 위에 있지만 CVAE는 그렇지 않은 것을 확인하실 수 있습니다. 이처럼, GVAE가 유효한 string으로 구성된 latent space를 더 잘 구축한다는 것입니다.

Table 2.은 각 latent space에서 z를 여러 번 샘플링 한 후, decoding 결과 유효한 수학표현식 또는 분자 string의 비율을 나타낸 것입니다. GVAE가 CVAE보다 문법적으로 의미있는 string을 더 잘 출력함을 확인할 수 있습니다.

그림 7의 결과는 penalized logP와 latent vector를 가지고 Bayesian Optimization한 결과, penalized logP score가 높은 순으로 3개를 뽑은 결과입니다. CVAE와 GVAE 모두 유효한 string을 내놨을 때, GVAE의 약물 특성에 관한 score가 더 높습니다. 즉, GVAE를 Bayesian Optimization까지 완료 후 형성된 latent space는 valid한 string을 내뱉는 공간을 형성했을 뿐만 아니라 약물 특성을 잘 포함하는 공간을 구축했음을 의미합니다.

그림 8의 결과는 약물 특성(penalized logP)에 관한 예측 성능에 관한 표입니다. Loss function을 Log-Likelihood와 RMSE를 모두 사용했을 때, GVAE가 CVAE보다 성능이 더 낫습니다. 다만, 개인적인 의견으로는 두개의 성능 차이는 거의 나지 않는 것으로 보입니다.

논문 한줄 리뷰평

GVAE는 이제까지 여러 Generative Model이 상당 수가 SMILES 문법에 어긋나는 string을 출력한다라는 단점을 보완하는 논문입니다. 하지만 valid한 string이 얼마나 신약개발에 적합한 string인지에 대한 결과는 논문에 실리지 않았습니다(이 부분은 대부분의 신약개발 논문들이 나와있지 않는 것으로 보입니다.). 하지만 valid한 string을 내놓는 것에 있어서 제일 실용적인(practical)하지도 않을까 생각이 듭니다.